如何用正则表达式匹配 3 的倍数
问题背景
最近在知乎上看到这样一个问题『如何用正则表达式匹配 3 的倍数』,原帖给出的答案非常有意思,遂研究了一番
看一个数能否被 3 整除,最直接的办法就是将这个数用 3 除一下,如果余数是 0,那么这个数就可以被3 整除。然而正则并不具有计算的功能,正则算法的实现基于有穷状态自动机(finite automaton)
以下是一个简单的示例
这正则表达式 哈+嗝 的自动机,该正则表达式可以匹配一连串的『哈』紧接着一个『嗝』
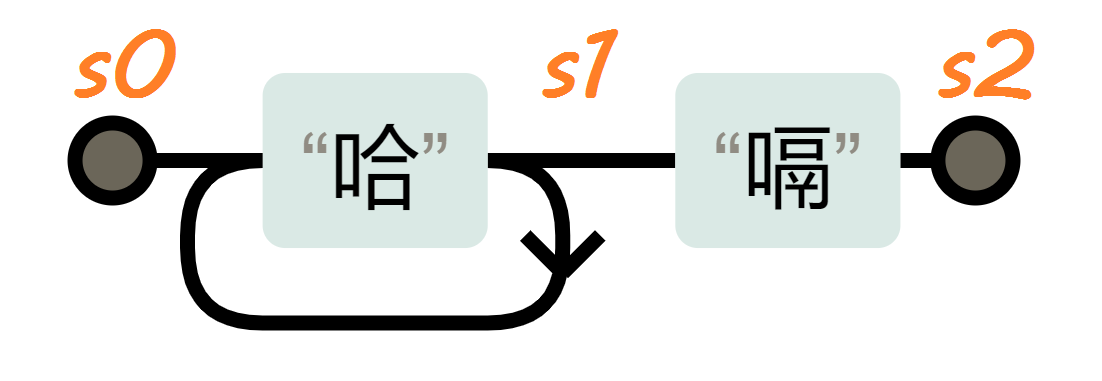
该自动机从左到右遍历一个字符串。可以看到,自动机初始状态是 s0,当遇到一个『哈』时,其状态变为 s1。此时,如果后面的字符还是『哈』,那么该自动机的状态会不断地在 s0 和 s1 之间转换,直到遇到一个不是『哈』的字符,状态稳定在 s1。此时如果下一个字符是『嗝』,则自动机变为状态 s2,也就是说该自动机匹配到了一个指定的文本;如果是其他字符,则匹配失败,回到 s0。
我们常说一个正则表达式匹配到了文本,就是在文本中寻找一个字符串,可以让该正则表达式的自动机从起始状态转移到结束状态。如果我们要解决文章开头提出的问题,就要设计出合适的自动机。
设计自动机
我们来分析一下手动计算除法的过程
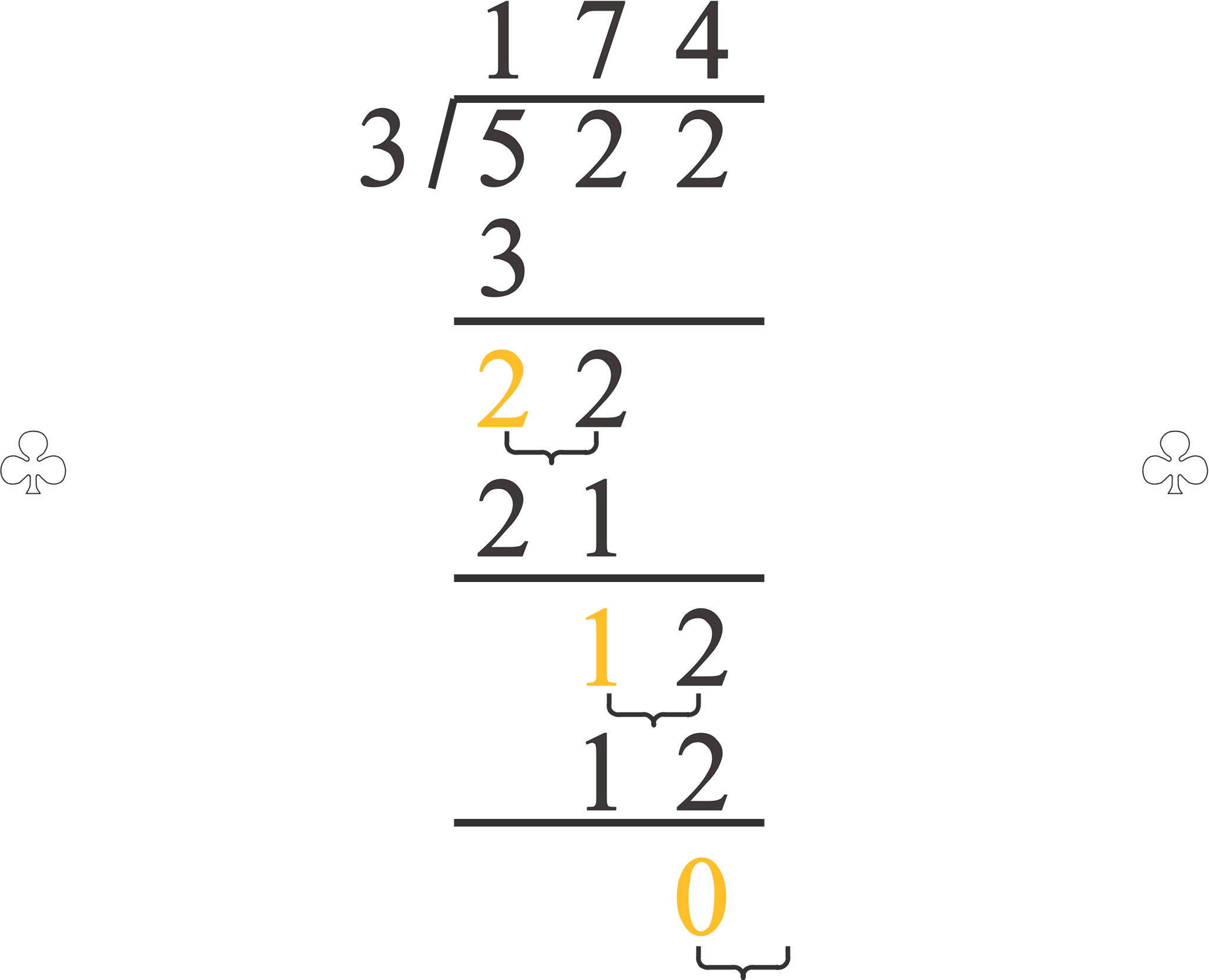
仔细观察上图,可以发现一个数被 3 除,余数只有 0,1,2 三种情况,此时被除数的下一位可以是 0 ~ 9 的任意一值,也即我们需要处理的范围只有 00 ~ 09,1029。
此时,我们已经有了一个自动机的雏形,它包括 A,B,C 三个状态

由于我们的规则只有 00 ~ 09,1029,共 30 种,所以可以直接将这些规则添加到自动机中。这个自动机开始状态和结束状态都是 A

对于前面的示例 522/3 ,在状态机中经过的路径如下,可以看到最终返回到了状态 A,表示 522 可以被 3 整除。

状态机转正则表达式
下面来看看如何将我们设计出的这个状态机转换为正则表达式。有一点需要注意,由于我们的状态机起始状态和终止状态都为 A,如果在开始状态什么事都不做,实际已经处于终止状态,也就是说我们的状态机可以匹配到空字符串。在下面的推导中,我将用『Ø』表示空字符串。
我们假定 A 是一个可以让状态机由终止状态转换到状态 A 的字符串,BC 类似。根据状态机可以列出如下三个方程
A = A[0369] | B[258] | C[147] | Ø
B = A[147] | B[0369] | C[258]
C = A[258] | B[147] | C[0369]
要从这三个方程推导出我们想要的正则表达式需要下面两个技巧
技巧1:根据正则语言的特性给定如下形式的方程,和它的解,以下每个字母均代表一个正则表达式
L = LU | V
解:L = VU*
我们将解带入原方程可验证它的正确性
VU* = VU*U | V
VU* = VU+ | V
技巧2:分配律
(U | V) A = UA | VA
根据这两个技巧,推导过程如下,你可以暂时跳过这个推导过程
上述方程可以修改为:
A = (Ø | B[258] | C[147])[0369]* (1)
B = (A[147] | C[258])[0369]* (2)
C = (A[258] | B[147])[0369]* (3)
将 (3) 代入 (1)(2) 得
A = (Ø | B[258] | (A[258] | B[147])[0369]*[147])[0369]* (4)
B = (A[147] | (A[258] | B[147])[0369]*[258])[0369]* (5)
用分配律展开 (5) 中的竖线得到
B = A[147][0369]* | A[258][0369]*[258][0369]* | B[147][0369]*[258][0369]*
= B[147][0369]*[258][0369]* | A[147][0369]* | A[258][0369]*[258][0369]*
= (A[147][0369]* | A[258][0369]*[258][0369]*)([147][0369]*[258][0369]*)*
= A[147][0369]*([147][0369]*[258][0369]*)* | A[258][0369]*[258][0369]*([147][0369]*[258][0369]*)*
把它代入 (4) 得
A = (Ø | B[258] | (A[258] | B[147])[0369]*[147])[0369]*
= [0369]* | B[258][0369]* | (A[258] | B[147])[0369]*[147][0369]*
= [0369] | B[258][0369]* | A[258][0369]*[147][0369]* | B[147][0369]*[147][0369]*
= [0369]*
| B[258][0369]*
| A[258][0369]*[147][0369]*
| B[147][0369]*[147][0369]*
= [0369]*
| A[147][0369]*([147][0369]*[258][0369]*)*[258][0369]*
| A[258][0369]*[258][0369]*([147][0369]*[258][0369]*)*[258][0369]*
| A[258][0369]*[147][0369]*
| A[147][0369]*([147][0369]*[258][0369]*)*[147][0369]*[147][0369]*
| A[258][0369]*[258][0369]*([147][0369]*[258][0369]*)*[147][0369]*[147][0369]*
= A[...] | [0369]*
= [0369]* [...]*
= [0369]* (
[147][0369]*([147][0369]*[258][0369]*)*[258][0369]*
| [258][0369]*[258][0369]*([147][0369]*[258][0369]*)*[258][0369]*
| [147][0369]*([147][0369]*[258][0369]*)*[147][0369]*[147][0369]*
| [258][0369]*[258][0369]*([147][0369]*[258][0369]*)*[147][0369]*[147][0369]*
| [258][0369]*[147][0369]* )*
= [0369]* (
([147][0369]* | [258][0369]*[258][0369]*)
([147][0369]*[258][0369]*)*
([258][0369]* | [147][0369]*[147][0369]*)
| [258][0369]*[147][0369]*
)*
以上就是我们得到的正则表达式,我们去掉结果中的换行与空格,用 (?:) 消去不必要的子组,再加上断言 (?<!\d) 与 (?!\d) 确保匹配整个数字,得到最终的正则表达式如下:
(?<!\d)[0369]*(?:(?:[147][0369]*|[258][0369]*[258][0369]*)(?:[147][0369]*[258][0369]*)*(?:[258][0369]*|[147][0369]*[147][0369]*)|[258][0369]*[147][0369]*)*(?!\d)
这是该正则表达式真正的自动机,该自动机将开始状态与结束状态区分开了
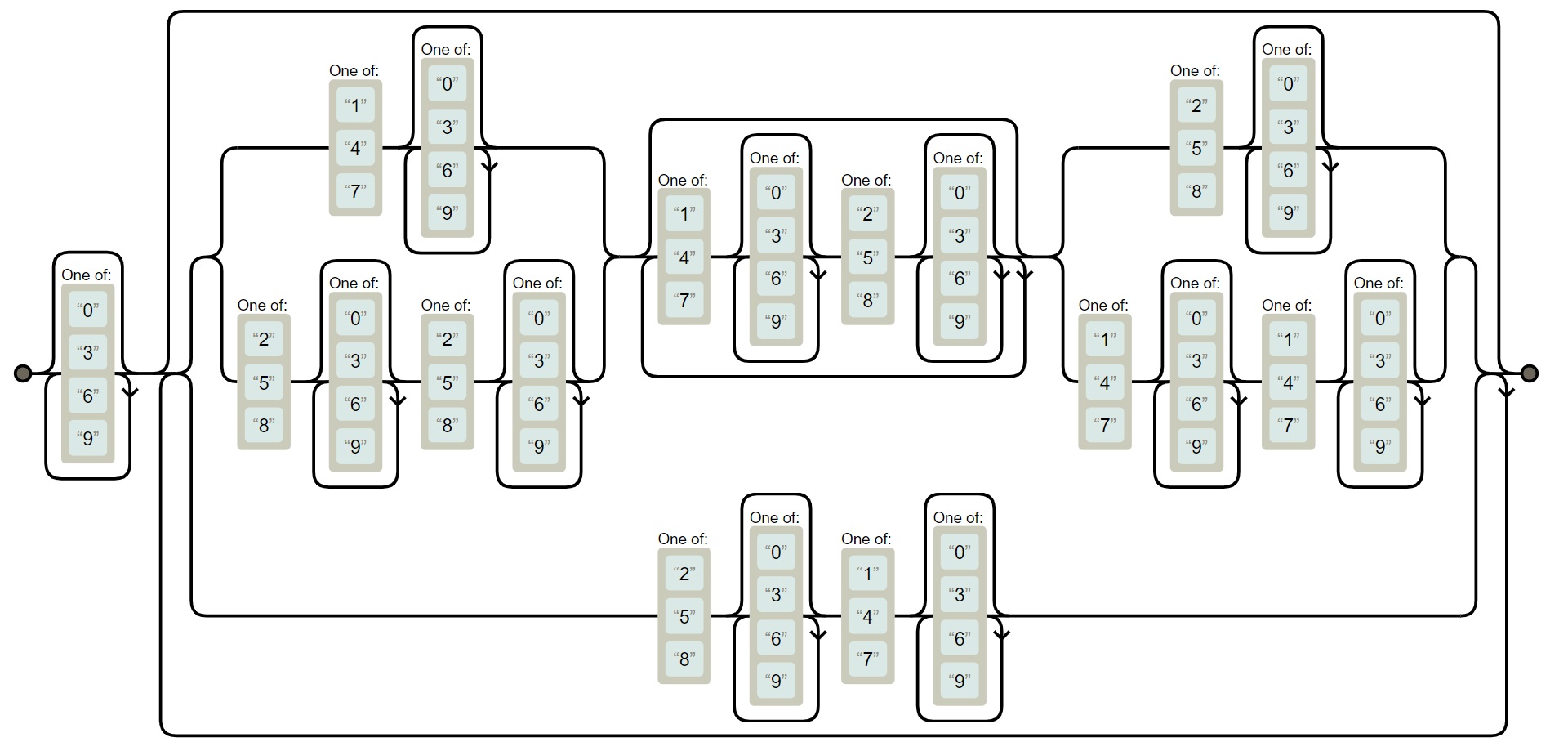
有点儿复杂,但是我们知道 3 的倍数有一个特性:如果一个数可以被 3 整除,那么这个数各位之和也能被 3 整除,反之也成立。我们在各位数中剔除『0,3,6,9』这些本身就是 3 的倍数的元素,将剩下元素的加和并不会影响我们的判断。就是说正则中的 [0369]* 实际上对理清该正则表达式没有帮助,我们暂时忽略正则中所有的 [0369]* ,得到如下状态机
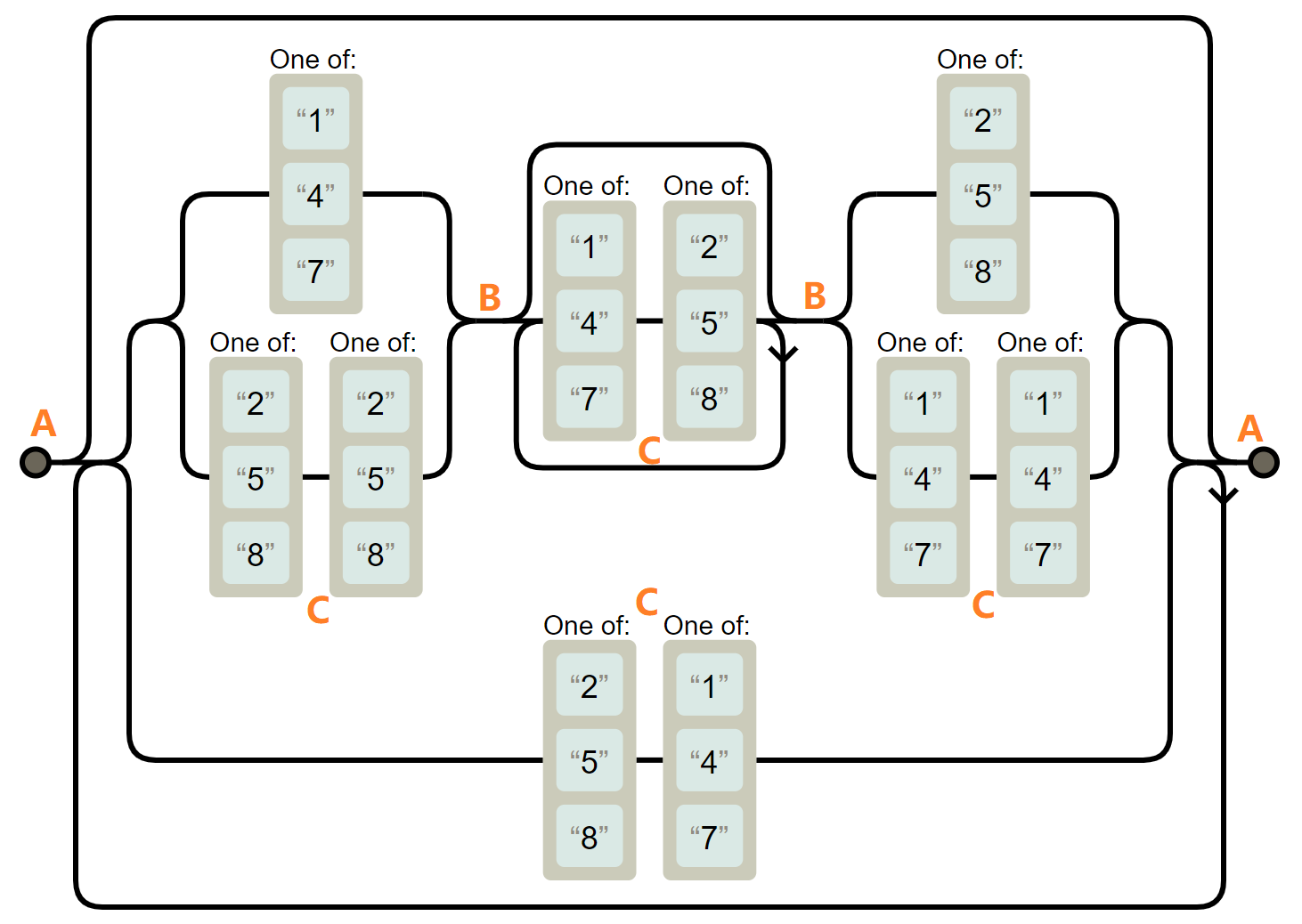
我将该状态机与我们开头所设计的状态机对应的状态标记在了图像上,以便于你理解我们推导的正则表达式。
更一般的情况
如和用正则表达式匹配十进制下任意一个整数的倍数呢?
实际上前面讲述的思路可以用于匹配任一个整数 n 的倍数,我们就需要构造一个有 n 个状态的自动机
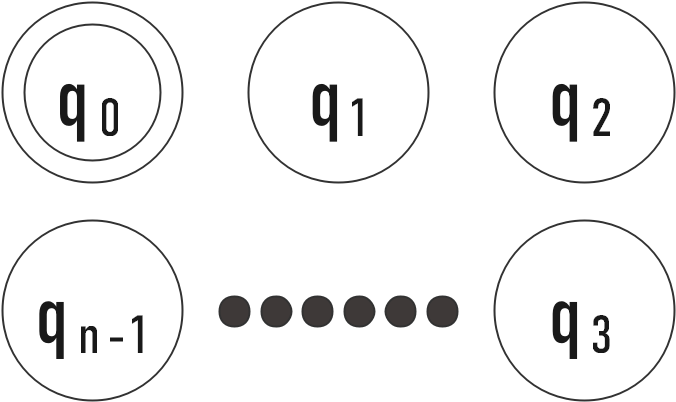
在这个状态机中,起始状态和结束状态都是『q0』,第 k 个状态『qk』代表当前读入的数可以被 n 除余 k。我们将手算除法扩展到一般形式:
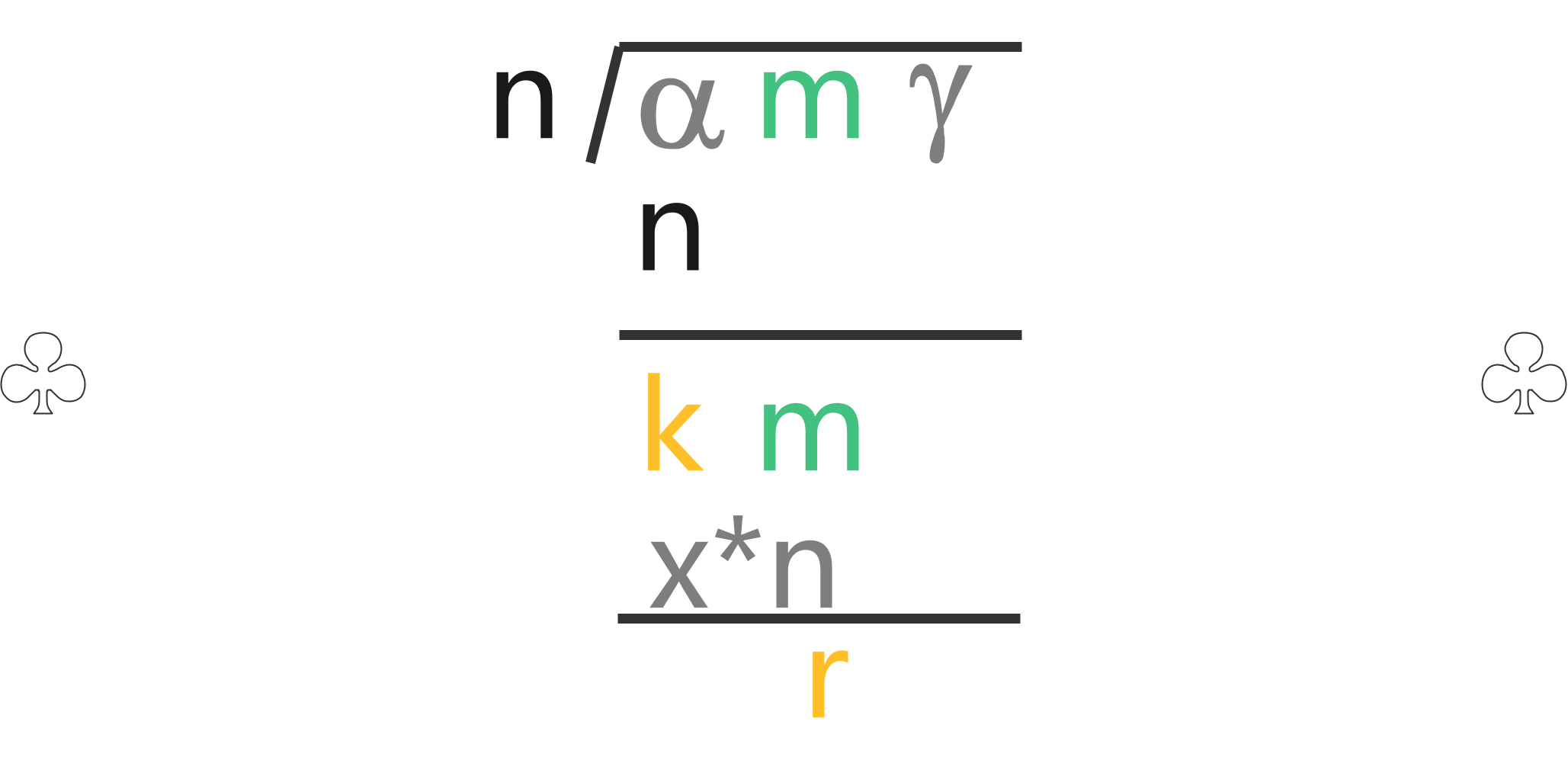
前面讨论过 m 的范围是 [ 0 - 9 ],易得通过如下的公式即可构造一条从『qk』到『qr』的转移边
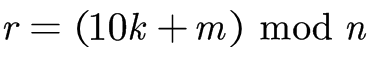
我们需要对每个状态『qk』和 m 的组合都用这个公式计算一遍,这样才可以求得所有的转移边,工作量等于
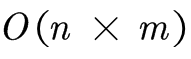
当然实际编程中我们并不会用这个方法来匹配某一个数的倍数,这里探讨这一问题仅用于拓展思路。
正则表达式如何匹配 3 的倍数? - Belleve的回答 - 知乎 https://www.zhihu.com/question/24824487/answer/29109747